The last time this came up, one suggestion was to use software that palette matched without the 256 limit, like Krita. Another was to search Github for tools specific to emulating the Genesis.
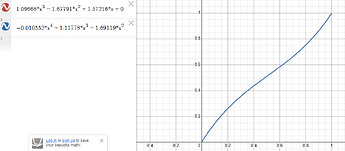
If I wanted to stick with Aseprite and to avoid all the problems that come with matching to a palette, then I’d try to reproduce the math formula for the curve shown on the website that you linked. That’s beyond my maths knowledge, so I went to a website that did curve fitting from a table of x, y data (https://www.dcode.fr/function-equation-finder).
Below is a preparatory script to test the math formulas from that site:
Click on the arrow to the left to see Lua code
local linear8 <const> = {
[1] = 0,
[2] = 18,
[3] = 36,
[4] = 55,
[5] = 73,
[6] = 91,
[7] = 109,
[8] = 128,
[9] = 146,
[10] = 164,
[11] = 182,
[12] = 200,
[13] = 219,
[14] = 237,
[15] = 255
}
local linear01 <const> = {
[1] = 0.0,
[2] = 0.070588235294118,
[3] = 0.14117647058824,
[4] = 0.2156862745098,
[5] = 0.28627450980392,
[6] = 0.35686274509804,
[7] = 0.42745098039216,
[8] = 0.50196078431373,
[9] = 0.57254901960784,
[10] = 0.64313725490196,
[11] = 0.71372549019608,
[12] = 0.7843137254902,
[13] = 0.85882352941176,
[14] = 0.92941176470588,
[15] = 1.0,
}
local sega8 <const> = {
[1] = 0,
[2] = 29,
[3] = 52,
[4] = 70,
[5] = 87,
[6] = 101,
[7] = 116,
[8] = 130,
[9] = 144,
[10] = 158,
[11] = 172,
[12] = 187,
[13] = 206,
[14] = 228,
[15] = 255
}
local sega01 <const> = {
[1] = 0.0,
[2] = 0.11372549019608,
[3] = 0.20392156862745,
[4] = 0.27450980392157,
[5] = 0.34117647058824,
[6] = 0.39607843137255,
[7] = 0.45490196078431,
[8] = 0.50980392156863,
[9] = 0.56470588235294,
[10] = 0.61960784313725,
[11] = 0.67450980392157,
[12] = 0.73333333333333,
[13] = 0.8078431372549,
[14] = 0.89411764705882,
[15] = 1.0,
}
print("\nReference")
print("| linear | sega |")
print("| -----: | ---: |")
local h = 0
while h < 15 do
h = h + 1
print(string.format("|%d|%d|", linear8[h], sega8[h]))
end
print("\nLinear to Sega")
print("|x|x8|y cubic|y8 cubic|y quartic|y8 quartic|")
print("|---:|---:|---:|---:|---:|---:|")
---@param x number
---@return number
local function linearToSegaCubic(x)
if x <= 0.0 then return 0.0 end
if x >= 1.0 then return 1.0 end
local xe2 <const> = x * x
local xe3 <const> = xe2 * x
local y <const> = 1.09668 * xe3
- 1.67791 * xe2
+ 1.57216 * x
+ 0.00524086
return y or 0.0
end
---@param x number
---@return number
local function linearToSegaQuartic(x)
if x <= 0.0 then return 0.0 end
if x >= 1.0 then return 1.0 end
local xe2 <const> = x * x
local xe3 <const> = xe2 * x
local xe4 <const> = xe3 * x
local y = -0.010552 * xe4
+ 1.11778 * xe3
- 1.69119 * xe2
+ 1.57489 * x
+ 0.00514704
return y or 0.0
end
local i = 0
while i < 15 do
i = i + 1
local x = linear01[i]
local yCubic = linearToSegaCubic(x)
local yQuartic = linearToSegaQuartic(x)
print(string.format("|%.4f|%d|%.4f|%d|%.4f|%d|",
x, math.floor(x * 255 + 0.5),
yCubic, math.floor(yCubic * 255 + 0.5),
yQuartic, math.floor(yQuartic * 255 + 0.5)))
end
print("\nSega to Linear")
print("|x|x8|y cubic|y8 cubic|y quartic|y8 quartic|")
print("|---:|---:|---:|---:|---:|---:|")
---@param x number
---@return number
local function segaToLinearCubic(x)
if x <= 0.0 then return 0.0 end
if x >= 1.0 then return 1.0 end
local xe2 <const> = x * x
local xe3 <const> = xe2 * x
local y <const> = -1.20393 * xe3
+ 1.85109 * xe2
+ 0.348584 * x
+ 0.00318634
return y or 0.0
end
---@param x number
---@return number
local function segaToLinearQuartic(x)
if x <= 0.0 then return 0.0 end
if x >= 1.0 then return 1.0 end
local xe2 <const> = x * x
local xe3 <const> = xe2 * x
local xe4 <const> = xe3 * x
local y = -0.186631 * xe4
- 0.830638 * xe3
+ 1.61616 * xe2
+ 0.396806 * x
+ 0.00170183
return y or 0.0
end
local j = 0
while j < 15 do
j = j + 1
local x = sega01[j]
local yCubic = segaToLinearCubic(x)
local yQuartic = segaToLinearQuartic(x)
print(string.format("|%.4f|%d|%.4f|%d|%.4f|%d|",
x, math.floor(x * 255 + 0.5),
yCubic, math.floor(yCubic * 255 + 0.5),
yQuartic, math.floor(yQuartic * 255 + 0.5)))
end
The tables output by the script:
Click on the arrow to the left to see results tables
Reference
| linear | sega |
|---|---|
| 0 | 0 |
| 18 | 29 |
| 36 | 52 |
| 55 | 70 |
| 73 | 87 |
| 91 | 101 |
| 109 | 116 |
| 128 | 130 |
| 146 | 144 |
| 164 | 158 |
| 182 | 172 |
| 200 | 187 |
| 219 | 206 |
| 237 | 228 |
| 255 | 255 |
Linear to Sega
| x | x8 | y cubic | y8 cubic | y quartic | y8 quartic |
|---|---|---|---|---|---|
| 0.0000 | 0 | 0.0000 | 0 | 0.0000 | 0 |
| 0.0706 | 18 | 0.1082 | 28 | 0.1083 | 28 |
| 0.1412 | 36 | 0.1968 | 50 | 0.1969 | 50 |
| 0.2157 | 55 | 0.2773 | 71 | 0.2773 | 71 |
| 0.2863 | 73 | 0.3435 | 88 | 0.3436 | 88 |
| 0.3569 | 91 | 0.4024 | 103 | 0.4024 | 103 |
| 0.4275 | 109 | 0.4563 | 116 | 0.4563 | 116 |
| 0.5020 | 128 | 0.5103 | 130 | 0.5103 | 130 |
| 0.5725 | 146 | 0.5612 | 143 | 0.5611 | 143 |
| 0.6431 | 164 | 0.6141 | 157 | 0.6140 | 157 |
| 0.7137 | 182 | 0.6713 | 171 | 0.6713 | 171 |
| 0.7843 | 200 | 0.7353 | 187 | 0.7353 | 188 |
| 0.8588 | 219 | 0.8126 | 207 | 0.8126 | 207 |
| 0.9294 | 237 | 0.8975 | 229 | 0.8975 | 229 |
| 1.0000 | 255 | 1.0000 | 255 | 1.0000 | 255 |
Sega to Linear
| x | x8 | y cubic | y8 cubic | y quartic | y8 quartic |
|---|---|---|---|---|---|
| 0.0000 | 0 | 0.0000 | 0 | 0.0000 | 0 |
| 0.1137 | 29 | 0.0650 | 17 | 0.0665 | 17 |
| 0.2039 | 52 | 0.1410 | 36 | 0.1425 | 36 |
| 0.2745 | 70 | 0.2135 | 54 | 0.2142 | 55 |
| 0.3412 | 87 | 0.2898 | 74 | 0.2897 | 74 |
| 0.3961 | 101 | 0.3568 | 91 | 0.3562 | 91 |
| 0.4549 | 116 | 0.4315 | 110 | 0.4305 | 110 |
| 0.5098 | 130 | 0.5025 | 128 | 0.5014 | 128 |
| 0.5647 | 144 | 0.5735 | 146 | 0.5726 | 146 |
| 0.6196 | 158 | 0.6434 | 164 | 0.6429 | 164 |
| 0.6745 | 172 | 0.7110 | 181 | 0.7111 | 181 |
| 0.7333 | 187 | 0.7795 | 199 | 0.7803 | 199 |
| 0.8078 | 206 | 0.8581 | 219 | 0.8596 | 219 |
| 0.8941 | 228 | 0.9341 | 238 | 0.9355 | 239 |
| 1.0000 | 255 | 1.0000 | 255 | 1.0000 | 255 |
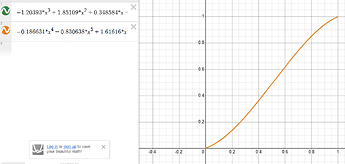
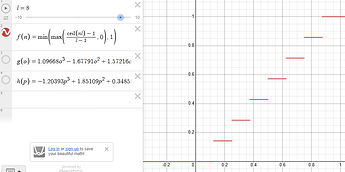
The results of the math formula are not exact. There is a tradeoff between accuracy and the number of calculations the computer has to do. Below are graphics for cubic and quartic. Since they overlap, I went with cubic.
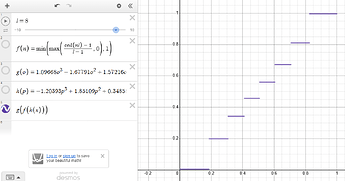
Then I’d take a posterization / quantization formula:
And combine:
This is a simplified quantize script that works on the active image, no dithering, no optimization, no UI to change inputs:
Click on the arrow to the left to see Lua code
local sprite <const> = app.sprite
if not sprite then return end
local colorMode <const> = sprite.colorMode
if colorMode ~= ColorMode.RGB then
print("Only RGB color mode supported.")
return
end
local layer <const> = app.layer
if not layer then return end
if layer.isReference then
print("Reference layers not supported.")
return
end
if layer.isTilemap then
print("Tile maps not supported.")
return
end
local frame <const> = app.frame
if not frame then return end
local cel <const> = layer:cel(frame)
if not cel then
print("No cel at this frame on this layer.")
return
end
local srcImage <const> = cel.image
local trgImage <const> = Image(srcImage)
local wImage <const> = srcImage.width
local hImage <const> = srcImage.height
---@param x number
---@return number
local function linearToSegaCubic(x)
if x <= 0.0 then return 0.0 end
if x >= 1.0 then return 1.0 end
local xe2 <const> = x * x
local xe3 <const> = xe2 * x
local y <const> = 1.09668 * xe3
- 1.67791 * xe2
+ 1.57216 * x
+ 0.00524086
return y or 0.0
end
---@param x number
---@return number
local function segaToLinearCubic(x)
if x <= 0.0 then return 0.0 end
if x >= 1.0 then return 1.0 end
local xe2 <const> = x * x
local xe3 <const> = xe2 * x
local y <const> = -1.20393 * xe3
+ 1.85109 * xe2
+ 0.348584 * x
+ 0.00318634
return y or 0.0
end
---@param x number
---@param l integer
---@return number
local function quantizeUnsigned(x, l)
return math.min(math.max(
(math.ceil(x * l) - 1.0) / (l - 1.0),
0.0), 1.0)
end
for y = 0, hImage - 1, 1 do
for x = 0, wImage - 1, 1 do
local abgr32Src <const> = trgImage:getPixel(x, y)
local a8Src <const> = app.pixelColor.rgbaA(abgr32Src)
local abgr32Trg = 0
if a8Src > 0 then
local r8Src <const> = app.pixelColor.rgbaR(abgr32Src)
local g8Src <const> = app.pixelColor.rgbaG(abgr32Src)
local b8Src <const> = app.pixelColor.rgbaB(abgr32Src)
local r01Src <const> = r8Src / 255.0
local g01Src <const> = g8Src / 255.0
local b01Src <const> = b8Src / 255.0
local r01Linear <const> = segaToLinearCubic(r01Src)
local g01Linear <const> = segaToLinearCubic(g01Src)
local b01Linear <const> = segaToLinearCubic(b01Src)
local r01Quantized <const> = quantizeUnsigned(r01Linear, 8)
local g01Quantized <const> = quantizeUnsigned(g01Linear, 8)
local b01Quantized <const> = quantizeUnsigned(b01Linear, 8)
local r01Sega <const> = linearToSegaCubic(r01Quantized)
local g01Sega <const> = linearToSegaCubic(g01Quantized)
local b01Sega <const> = linearToSegaCubic(b01Quantized)
local r8Trg <const> = math.floor(r01Sega * 255 + 0.5)
local g8Trg <const> = math.floor(g01Sega * 255 + 0.5)
local b8Trg <const> = math.floor(b01Sega * 255 + 0.5)
abgr32Trg = app.pixelColor.rgba(r8Trg, g8Trg, b8Trg, a8Src)
end
trgImage:drawPixel(x, y, abgr32Trg)
end
end
cel.image = trgImage
app.refresh()
I used a test image from https://github.com/seanbouk/quantizeMD/ which is a quantize tool mentioned in the other thread linked above.
Results for 8 (2^3) levels:
and 15 levels (the number of entries in the reference table):
Here are results from adding the Sega curve to a general dither script I had on hand. 8 levels:
15 levels:
I don’t do any retro homebrewing myself, but as I understand it there are more constraints than just bit depth, such as a color limit per a m x n tile. So there’s a limit to how well a general purpose dither can serve as a preview.
To compare, this is what the image looks like when processed through https://rilden.github.io/tiledpalettequant/. It seems to follow the tile constraint, but not to use the curve.