Hello folks,
I’m interested in using Aseprite to create normal maps for pixel art so I can add some depth to my pixel art, but it’s quite tricky. I’m following a this game for GameMaker: Using Normal Maps to Light Your 2D Game
So I was wondering if anyone has any tips or good tutorials for drawing out normal maps in Aseprite. A quick google search didn’t really reveal much.
Thanks.
There’s nothing special about normal maps. If you have experience drawing them manually in other software, that should transfer right over to Aseprite. If you only know how to draw them using separate channels, it’ll be a little tougher since Aseprite doesn’t support channels directly. Instead, you’d need to have your channels as separate layers, and draw with only pure R, G, and B hues in each appropriate channel (e.g. in the Red layer, all colours should have the form xx0000). If you set their layer blending modes to Addition, the end result is their combination as if they were channels.
A different approach, perhaps one more suitable to pixel art, is to decide a palette of normals ahead of time, so that your normals look somewhat blocky just like the pixel art, with lots of parallel surfaces owing due to the limited normal directions available. If you organize your swatches so that they correspond to a sphere (i.e. looking like a circle), you can just pick from there as needed. Then, you can just draw your normal map as you would any other pixel art with a fixed palette.
I don’t have experience drawing them in other programs. What I have been doing so far is just drawing my sprite and then having a new layer where I’m drawing the normal map using the built-in normal map color wheel set to “discrete”.
This has worked pretty well with my experiments so far, but I was wondering if anyone had a list of tips/best practices/etc so I don’t have to figure everything out for myself. I did find a lua script that automatically generates a normal map outline around a sprite that has been helpful though I don’t know how practical it will be once I start making stuff for real.
One approach to draw them is to draw the sprite lit from two different directions for each channel: left and right for Red (X), top and bottom for Green (Y), and front/behind for Blue (Z)*. Remember NOT to include cast/occlusion shadows, only draw form shadows, and don’t have any reflected light or speculars, just the form lighting. For the right, top, and back drawings (the upper part of each range), you should be using colours between 50% grey and full white. For the left, bottom, and front drawings (the lower part of each range), you should be using colours between full black and 50% grey. You can also use full black to full white for both, but then you’ll need to do some extra transformations to get the colour ranges.
You’d then Subtract the lighting that’s in the lower direction (left, bottom, front) from the lighting that’s in the upper direction (right, top, back). After that, you’d use these as your channels to get the resulting normal map.
* The Z (blue channel) lighting is tricky and you’ll probably need to iterate, and you probably don’t actually need a front-lit drawing, just a back-lit one, going from black to white.
Once you get the hang of this approach, you’ll be able to avoid the need for four-six drawings and can instead draw each channel on its own, requiring only two-three drawings.
As I mentioned in my previous post though, I think for pixel art, it probably looks best to just paint it directly using a sphere as a guide. However, if you don’t quite understand how normal maps work and how the way the map looks related to what you get in-engine, drawing a few using this approach might be helpful. It’s hard to choose the correct colours, even if you have a correctly organized palette, if you don’t quite understand what they mean. The key thing, though, is that the colours are just the sums of the three separate channels.
Also, check out Sprite Lamp’s website. Even if you don’t use the tool, the example drawings they provide should help give an idea of how the basic concept I described above works. Sprite Lamp uses 2 to 5 black-to-white drawings, from which it calculates the channels, but the same process can be done in any image editor. Aseprite just adds the extra steps I described before, since it doesn’t natively support channels.
Hi @D_W,
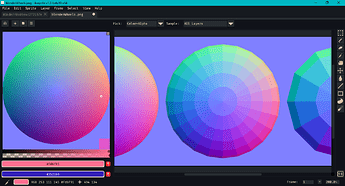
If it helps you to imagine that you’re looking down at a sphere’s North pole, I suggest comparing Aseprite’s normal map wheel with others online first. Maybe bring them in as a reference image or drag and drop two sprite tabs.
For example, this is an image looking down at 3 UV spheres that I made in Blender.
If the distribution of discrete swatches matters, icospheres or cube-spheres could be used instead.
I realize my eyedropper can’t be seen in the comparison below, so I encourage you to do your own comparison (using both smooth and discrete images).
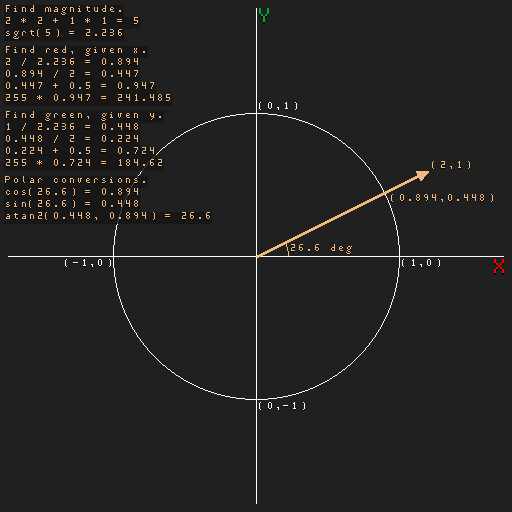
If knowing some of the math behind the colors would help, here’s a diagram simplified from 3D to 2D. This is for the vector (2, 1).
This should look familiar if you’ve taken a trigonometry class. A fuller 3D maths detail can be found in an entry on the spherical coordinate system. (3D coordinate systems vary across game engines and software; see the right-hand rule.)
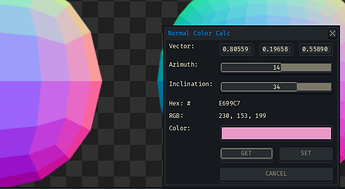
The math can be parlayed into a Lua color picker script. My preference would be to work in directions instead of trying to combine colors directly.
This script will calculate directions below an inclination of zero (at a normal sphere’s equator), though they are not used in normal maps.
local function fromSpherical(az, incl)
local a = az * math.pi / 180.0
local i = incl * math.pi / 180.0
local cosAzim = math.cos(a)
local sinAzim = math.sin(a)
local cosIncl = math.cos(i)
local sinIncl = math.sin(i)
return cosIncl * cosAzim,
cosIncl * sinAzim,
sinIncl
end
local function toSpherical(x, y, z)
local sqmag = x * x + y * y + z * z
if sqmag > 0.0 then
local azRad = math.atan(y, x)
local azDeg = azRad * 180.0 / math.pi
local inclRad = math.acos(z / math.sqrt(sqmag))
local inclDeg = inclRad * 180.0 / math.pi
inclDeg = 90.0 - inclDeg
return azDeg, inclDeg
else
return 0.0, 90.0
end
end
local function vecToColor(x, y, z)
local sqMag = x * x + y * y + z * z
if sqMag > 0.0 then
local mag = math.sqrt(sqMag)
local xn = x / mag
local yn = y / mag
local zn = z / mag
local r01 = xn * 0.5 + 0.5
local g01 = yn * 0.5 + 0.5
local b01 = zn * 0.5 + 0.5
local r255 = math.tointeger(0.5 + 255.0 * r01)
local g255 = math.tointeger(0.5 + 255.0 * g01)
local b255 = math.tointeger(0.5 + 255.0 * b01)
return Color(r255, g255, b255, 255)
else
return Color(128, 128, 255, 255)
end
end
local function updateWidgetClr(dialog, clr)
dialog:modify {
id = "normalColor",
colors = { clr } }
dialog:modify {
id = "hexCode",
text = string.format(
"%06X",
(clr.red << 0x10 |
clr.green << 0x08 |
clr.blue))
}
dialog:modify {
id = "rgbLabel",
text = string.format(
"%d, %d, %d",
clr.red,
clr.green,
clr.blue)
}
end
local function updateWidgetCart(dialog)
local args = dialog.data
local x = args.x
local y = args.y
local z = args.z
local a, i = toSpherical(x, y, z)
if a < 0.0 then a = a - 0.5 end
if a > 0.0 then a = a + 0.5 end
if i < 0.0 then i = i - 0.5 end
if i > 0.0 then i = i + 0.5 end
dialog:modify {
id = "azimuth",
value = math.tointeger(a)
}
dialog:modify {
id = "inclination",
value = math.tointeger(i)
}
local clr = vecToColor(x, y, z)
updateWidgetClr(dialog, clr)
end
local function updateWidgetSphere(dialog)
local args = dialog.data
local az = args.azimuth
local incl = args.inclination
local x, y, z = fromSpherical(az, incl)
dialog:modify { id = "x", text = string.format("%.5f", x) }
dialog:modify { id = "y", text = string.format("%.5f", y) }
dialog:modify { id = "z", text = string.format("%.5f", z) }
local clr = vecToColor(x, y, z)
updateWidgetClr(dialog, clr)
end
local dlg = Dialog { title = "Normal Color Calc" }
dlg:newrow { always = false }
dlg:number {
id = "x",
label = "Vector:",
text = string.format("%.5f", 0.0),
decimals = 5,
onchange = function()
updateWidgetCart(dlg)
end
}
dlg:number {
id = "y",
text = string.format("%.5f", 0.0),
decimals = 5,
onchange = function()
updateWidgetCart(dlg)
end
}
dlg:number {
id = "z",
text = string.format("%.5f", 1.0),
decimals = 5,
onchange = function()
updateWidgetCart(dlg)
end
}
dlg:newrow { always = false }
dlg:slider {
id = "azimuth",
label = "Azimuth:",
min = -180,
max = 180,
value = 0,
onchange = function()
updateWidgetSphere(dlg)
end
}
dlg:newrow { always = false }
dlg:slider {
id = "inclination",
label = "Inclination:",
min = -90,
max = 90,
value = 90,
onchange = function()
updateWidgetSphere(dlg)
end
}
dlg:newrow { always = false }
dlg: label {
id = "hexCode",
label = "Hex: #",
text = "8080FF"
}
dlg:newrow { always = false }
dlg: label {
id = "rgbLabel",
label = "RGB:",
text = "128, 128, 255"
}
dlg:newrow { always = false }
dlg:shades {
id = "normalColor",
label = "Color:",
mode = "sort",
colors = { Color(128, 128, 255, 255) }
}
dlg:newrow { always = false }
dlg:button {
id = "getColor",
text = "&GET",
onclick = function()
local clr = app.fgColor
local r255 = clr.red
local g255 = clr.green
local b255 = clr.blue
if clr.alpha < 1 then
r255 = 128
g255 = 128
b255 = 255
end
local r01 = r255 / 255.0
local g01 = g255 / 255.0
local b01 = b255 / 255.0
local x = r01 + r01 - 1.0
local y = g01 + g01 - 1.0
local z = b01 + b01 - 1.0
local sqmag = x * x + y * y + z * z
if sqmag > 0.0 then
local xn = x
local yn = y
local zn = z
local mag = math.sqrt(sqmag)
xn = x / mag
yn = y / mag
zn = z / mag
dlg:modify { id = "x", text = string.format("%.5f", xn) }
dlg:modify { id = "y", text = string.format("%.5f", yn) }
dlg:modify { id = "z", text = string.format("%.5f", zn) }
local a, i = toSpherical(xn, yn, zn)
if a < 0.0 then a = a - 0.5 end
if a > 0.0 then a = a + 0.5 end
if i < 0.0 then i = i - 0.5 end
if i > 0.0 then i = i + 0.5 end
dlg:modify {
id = "azimuth",
value = math.tointeger(a)
}
dlg:modify {
id = "inclination",
value = math.tointeger(i)
}
local nr01 = xn * 0.5 + 0.5
local ng01 = yn * 0.5 + 0.5
local nb01 = zn * 0.5 + 0.5
local nr255 = math.tointeger(0.5 + 255.0 * nr01)
local ng255 = math.tointeger(0.5 + 255.0 * ng01)
local nb255 = math.tointeger(0.5 + 255.0 * nb01)
dlg:modify {
id = "normalColor",
colors = { Color(nr255, ng255, nb255, 255) }
}
dlg:modify {
id = "hexCode",
text = string.format("%06X",
(nr255 << 0x10 |
ng255 << 0x08 |
nb255))
}
dlg:modify {
id = "rgbLabel",
text = string.format("%d, %d, %d",
nr255, ng255, nb255)
}
end
end
}
dlg:button {
id = "setColor",
text = "&SET",
onclick = function()
local normalColors = dlg.data.normalColor
if #normalColors > 0 then
local normalColor = normalColors[1]
app.fgColor = Color(
normalColor.red,
normalColor.green,
normalColor.blue,
255)
end
end
}
dlg:newrow { always = false }
dlg:button {
id = "cancel",
text = "&CANCEL",
onclick = function()
dlg:close()
end
}
dlg:show { wait = false }
If nothing else, this could be a stepping stone to understand the workings of the previous script that you used.
Ultimately, some 3D tool – such as those suggested in the tutorial you linked – would be helpful, if only to serve as a pre-visualization step.
Cheers,
Jeremy