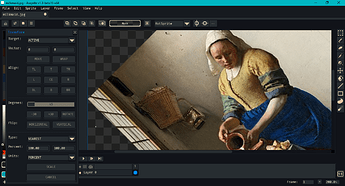
Hi all,
A while back, a problem with rotating by 90 degrees in Aseprite beta 1.3 was reported. On and off, I’ve been experimenting with a workaround in Lua. This is a write-up on my progress. While a lot of info on this subject can be found all over the Internet, good info was scattered and written in different programming languages.
The scripts below simplify a more involved dialog from here. What I’m showing in this post are problems and some approaches to address them.
Test image source - Vermeer, The Milkmaid
This post doesn’t address rotation around an arbitrary pivot.
Nor does it deal with animation. For that reason, I don’t talk about revolutions (for example, 720 degrees is 2 revolutions). If you’re interested in animated rotations, try Gasparoken’s rotar script instead. (Looks like it also handles arbitrary pivots.)
Conventions differ depending on (1.) whether you want a signed or unsigned range, [-180, 180] or [0, 360], as input; (2.) whether clockwise (CW) or counter-clockwise (CCW) is a positive angle rotation. I use [0, 360] and assume that the y-axis (0, 1) points up to the top of the screen. A positive angle is CCW.
In raster graphics, rotation involves a loss or invention of data in most cases. The exception is for rotations by 90 degree increments. Otherwise, integer values are promoted to real numbers, altered, then demoted back down to integers. If an image is rotated several times, errors accumulate.
The above image is from the built-in fast rotation. Each frame, the image is copied from the previous frame and rotated 30 degrees. The test image is from here.
The next image is created via script.
In the script, accumulated error impacts both the pixels in the image and the cel position. A new top-left corner is calculated from the center.
Because exception cases only involve pixel swapping, an image’s color mode doesn’t matter. I’m not going to address the issue where an image belongs to a tile map layer and has a special color mode.
This first exception is for 0 and 360 degrees of rotation. Nothing needs to be done to the image.
The second exception is to rotate an image by 180 degrees. To do this, an array of pixels is reversed. The reversal can be done in-place; no target array needs to be created. There might be a more efficient way of doing this if you don’t want to separate Aseprite specific functions from general functions that are easily adapted.
local function reverseTable(t)
-- https://programming-idioms.org/idiom/19/reverse-a-list/1314/lua
local n = #t
local i = 1
while i < n do
t[i], t[n] = t[n], t[i]
i = i + 1
n = n - 1
end
return t
end
local function rotateImage180(source)
local px = {}
local i = 0
local srcPxItr = source:pixels()
for elm in srcPxItr do
i = i + 1
px[i] = elm()
end
-- Table is reversed in-place.
reverseTable(px)
local target = Image(source.spec)
local j = 0
local trgPxItr = target:pixels()
for elm in trgPxItr do
j = j + 1
elm(px[j])
end
return target
end
local img = rotateImage180(app.activeCel.image)
app.activeCel.image = img
For 90 degrees, the original array is copied into a new one. A one dimensional index is converted to 2D coordinates with x = i % width and y = i // width. % can be either truncation or floor modulo, since i is assumed to be positive. // can be either integer or floor division for the same reason. Coordinates are transformed to an index with i = x + y * width. A reminder: in Lua, indices start at 1, not 0; tripartite for-loops are upper bound inclusive (<= not <).
Here is a simplified diagram of the swap:
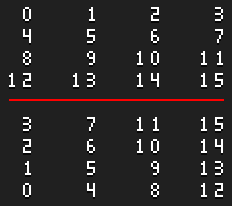
The image’s old width becomes it’s new height. Its old height becomes its new width. A cel’s position needs to be updated as well as its image. Also, I’d recommend debugging with a test image that has different width and height. ![]()
local function rotatePixels90(source, w, h)
local len = #source
local lennh = len - h
local rotated = {}
local i = 0
while i < len do
rotated[1 + lennh + (i // w) - (i % w) * h] = source[1 + i]
i = i + 1
end
return rotated
end
local function rotateImage90(source)
local px = {}
local i = 0
local srcPxItr = source:pixels()
for elm in srcPxItr do
i = i + 1
px[i] = elm()
end
local srcSpec = source.spec
local w = srcSpec.width
local h = srcSpec.height
local pxRot = rotatePixels90(px, w, h)
local trgSpec = ImageSpec {
width = h,
height = w,
colorMode = source.colorMode,
transparentColor = srcSpec.transparentColor }
trgSpec.colorSpace = srcSpec.colorSpace
local target = Image(trgSpec)
local j = 0
local trgPxItr = target:pixels()
for elm in trgPxItr do
j = j + 1
elm(pxRot[j])
end
return target
end
local img = rotateImage90(app.activeCel.image)
app.activeCel.image = img
local p = app.activeCel.position
local w_2 = img.width // 2
local h_2 = img.height // 2
app.activeCel.position = Point(
p.x + h_2 - w_2,
p.y + w_2 - h_2)
270 degrees follows a similar pattern.

local function rotatePixels270(source, w, h)
local len = #source
local hn1 = h - 1
local rotated = {}
local i = 0
while i < len do
rotated[1 + (i % w) * h + hn1 - (i // w)] = source[1 + i]
i = i + 1
end
return rotated
end
local function rotateImage270(source)
local px = {}
local i = 0
local srcPxItr = source:pixels()
for elm in srcPxItr do
i = i + 1
px[i] = elm()
end
local srcSpec = source.spec
local w = srcSpec.width
local h = srcSpec.height
local pxRot = rotatePixels270(px, w, h)
local trgSpec = ImageSpec {
width = h,
height = w,
colorMode = source.colorMode,
transparentColor = srcSpec.transparentColor }
trgSpec.colorSpace = srcSpec.colorSpace
local target = Image(trgSpec)
local j = 0
local trgPxItr = target:pixels()
for elm in trgPxItr do
j = j + 1
elm(pxRot[j])
end
return target
end
local img = rotateImage270(app.activeCel.image)
app.activeCel.image = img
local p = app.activeCel.position
local w_2 = img.width // 2
local h_2 = img.height // 2
app.activeCel.position = Point(
p.x + h_2 - w_2,
p.y + w_2 - h_2)
For rotation with bilinear interpolation, I found this article very informative
http://polymathprogrammer.com/2008/10/06/image-rotation-with-bilinear-interpolation/
though the follow-up was my main reference. The article’s code is written in C#.
A key lesson from the article is what not to do. In my original attempt, I looped through the source image pixels, rotated them, and assigned a color to the corresponding coordinates in the destination image. This resulted in an image filled with transparent holes because no color was assigned to them.
What this does instead is loop through the target image pixels and sample a rectangle around the source pixel. It mixes pixel colors horizontally, then vertically.
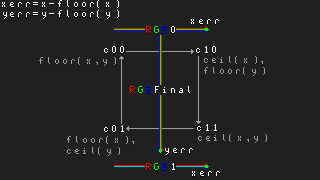
Here is a helper function to mix colors.
local function rgbMix(
rOrig, gOrig, bOrig, aOrig,
rDest, gDest, bDest, aDest, t)
if t <= 0.0 then return rOrig, gOrig, bOrig, aOrig end
if t >= 1.0 then return rDest, gDest, bDest, aDest end
local u = 1.0 - t
local aMix = u * aOrig + t * aDest
if aMix <= 0.0 then return 0.0, 0.0, 0.0, 0.0 end
local ro = rOrig
local go = gOrig
local bo = bOrig
if aOrig > 0.0 and aOrig < 255.0 then
local ao01 = aOrig / 255.0
ro = rOrig * ao01
go = gOrig * ao01
bo = bOrig * ao01
end
local rd = rDest
local gd = gDest
local bd = bDest
if aDest > 0.0 and aDest < 255.0 then
local ad01 = aDest / 255.0
rd = rDest * ad01
gd = gDest * ad01
bd = bDest * ad01
end
local rMix = u * ro + t * rd
local gMix = u * go + t * gd
local bMix = u * bo + t * bd
if aMix < 255.0 then
local aInverse = 255.0 / aMix
rMix = rMix * aInverse
gMix = gMix * aInverse
bMix = bMix * aInverse
end
return rMix, gMix, bMix, aMix
end
The source article did not address alpha premultiplication. Whether it’s necessary or whether I’ve done the best job of it, I don’t know. But to see what’s at issue, take this image

and rotate it by 45 degrees. Then put a high value background behind it. The dark haloing is evident.

Compare that with this

Unpremultiplying the mixed color without premultiplying the origin and destination colors will cause a white halo to develop through repeated rotations.
Regardless of the alpha issue, it’s a bad idea to mix color with sRGB. I’m using it because it’s fast and simple. Consider linear sRGB as an alternative. To illustrate, compare linear above with standard below:
![]()
Conversions can be done per channel via look-up tables. In Lua, I don’t know if a LUT provides any performance improvement, though.
local function rotBilinear(xSrc, ySrc, wSrc, hSrc, srcImg)
-- http://polymathprogrammer.com/2010/04/05/
-- image-rotation-with-bilinear-interpolation-and-no-clipping/
-- Sample four corners of source coordinate.
local yf = math.floor(ySrc)
local yc = math.ceil(ySrc)
local xf = math.floor(xSrc)
local xc = math.ceil(xSrc)
-- Find fractional difference between real
-- number and its floored integer. These will
-- be the color mixing factors.
local yErr = ySrc - yf
local xErr = xSrc - xf
local yfInBounds = yf > -1 and yf < hSrc
local ycInBounds = yc > -1 and yc < hSrc
local xfInBounds = xf > -1 and xf < wSrc
local xcInBounds = xc > -1 and xc < wSrc
local c00 = 0x0
local c10 = 0x0
local c11 = 0x0
local c01 = 0x0
-- Out of bounds is handled differently here
-- than in source article.
if xfInBounds and yfInBounds then
c00 = srcImg:getPixel(xf, yf)
end
if xcInBounds and yfInBounds then
c10 = srcImg:getPixel(xc, yf)
end
if xcInBounds and ycInBounds then
c11 = srcImg:getPixel(xc, yc)
end
if xfInBounds and ycInBounds then
c01 = srcImg:getPixel(xf, yc)
end
local r00 = app.pixelColor.rgbaR(c00)
local g00 = app.pixelColor.rgbaG(c00)
local b00 = app.pixelColor.rgbaB(c00)
local a00 = app.pixelColor.rgbaA(c00)
local r10 = app.pixelColor.rgbaR(c10)
local g10 = app.pixelColor.rgbaG(c10)
local b10 = app.pixelColor.rgbaB(c10)
local a10 = app.pixelColor.rgbaA(c10)
-- Mix top left to top right.
local r0, g0, b0, a0 = rgbMix(
r00, g00, b00, a00,
r10, g10, b10, a10, xErr)
local r01 = app.pixelColor.rgbaR(c01)
local g01 = app.pixelColor.rgbaG(c01)
local b01 = app.pixelColor.rgbaB(c01)
local a01 = app.pixelColor.rgbaA(c01)
local r11 = app.pixelColor.rgbaR(c11)
local g11 = app.pixelColor.rgbaG(c11)
local b11 = app.pixelColor.rgbaB(c11)
local a11 = app.pixelColor.rgbaA(c11)
-- Mix bottom left to bottom right.
local r1, g1, b1, a1 = rgbMix(
r01, g01, b01, a01,
r11, g11, b11, a11, xErr)
-- Mix top and bottom.
local rt, gt, bt, at = rgbMix(
r0, g0, b0, a0,
r1, g1, b1, a1, yErr)
-- Round to integer.
at = math.floor(0.5 + at)
bt = math.floor(0.5 + bt)
gt = math.floor(0.5 + gt)
rt = math.floor(0.5 + rt)
-- Clamp to [0, 255]
if at < 0 then at = 0 elseif at > 255 then at = 255 end
if bt < 0 then bt = 0 elseif bt > 255 then bt = 255 end
if gt < 0 then gt = 0 elseif gt > 255 then gt = 255 end
if rt < 0 then rt = 0 elseif rt > 255 then rt = 255 end
return app.pixelColor.rgba(rt, gt, bt, at)
end
For any image rotation by an arbitrary angle, a challenge is how to adjust the size of the destination image. If the destination image is too small, pixels will be clipped, or worse, there’ll be an out-of-bounds exception. If an image’s size is increased every rotation, and an image is rotated multiple times, then the final result will be massive.
After every rotation, an image’s alpha needs trimming, ideally without clipping it to the sprite bounds. I have an old post on the subject; I’ve since updated relevant scripts here and here. If you don’t care about clipping to sprite bounds, see app.command.CanvasSize. The parameter trimOutside should be true. You could also try trimming the source image prior to rotation.
While the above article was great, I preferred another article’s calculation for the new image dimensions. Here is a remake of the relevant diagram.
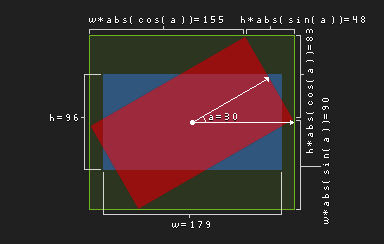
Take the axis-aligned-bounding-box (AABB) – in green – and subtract the rotated rectangle – in red – to get four right triangles (or two triangles and their reflections). The hypotenuses of these triangles are known from the original rectangle’s dimensions – in blue. Find the triangles’ legs with the help of the angle and the hypotenuses.
Unlike the C# source, the Lua port avoids atan2, cos, sin and sqrt to convert between Cartesian and polar coordinates when looping over each pixel.
local degrees = math.random(0, 360)
-- Flip y axis to be up, not down.
local radians = math.rad(360 - degrees)
local cosa = math.cos(radians)
local sina = -math.sin(radians)
local cel = app.activeCel
local srcImg = cel.image
local srcSpec = srcImg.spec
local wSrc = srcSpec.width
local hSrc = srcSpec.height
local alphaMask = srcSpec.transparentColor
-- Calculate new image dimensions.
local absCosa = math.abs(cosa)
local absSina = math.abs(sina)
local wTrg = math.floor(hSrc * absSina + wSrc * absCosa)
local hTrg = math.floor(hSrc * absCosa + wSrc * absSina)
local xSrcCenter = wSrc * 0.5
local ySrcCenter = hSrc * 0.5
local xTrgCenter = wTrg * 0.5
local yTrgCenter = hTrg * 0.5
local wDiffHalf = xTrgCenter - xSrcCenter
local hDiffHalf = yTrgCenter - ySrcCenter
local trgSpec = ImageSpec {
width = wTrg,
height = hTrg,
colorMode = srcSpec.colorMode,
transparentColor = alphaMask
}
trgSpec.colorSpace = srcSpec.colorSpace
local trgImg = Image(trgSpec)
-- Iterate through target pixels and read
-- from source pixels. Iterating through
-- source pixels leads to a rotation with
-- gaps in the pixels.
local trgPxItr = trgImg:pixels()
for elm in trgPxItr do
local xSgn = elm.x - xTrgCenter
local ySgn = elm.y - yTrgCenter
local xRot = cosa * xSgn - sina * ySgn
local yRot = cosa * ySgn + sina * xSgn
local xSrc = xSrcCenter + xRot
local ySrc = ySrcCenter + yRot
elm(rotBilinear(xSrc, ySrc, wSrc, hSrc, srcImg))
end
-- One possible location for alpha trim is here.
local srcPos = cel.position
cel.position = Point(
math.floor(srcPos.x - wDiffHalf),
math.floor(srcPos.y - hDiffHalf))
cel.image = trgImg
The biggest disadvantage of the bilinear method imo is that the anti-aliasing isn’t in the spirit of pixel art. Another big disadvantage is that it only handles RGB color mode. While it could be refitted to handle gray color mode, it won’t really work on indexed color mode.
local function rotNearest(xSrc, ySrc, wSrc, hSrc, srcImg)
local xr = math.floor(xSrc)
local yr = math.floor(ySrc)
if yr > -1 and yr < hSrc
and xr > -1 and xr < wSrc then
return srcImg:getPixel(xr, yr)
end
return 0x0
end
The above could be substituted in to handle such concerns. Replace math.floor with whatever rounding method you find appropriate.
A lot of articles on the subject I found focused on a double shear (or skew) algorithm attributed to Alan W. Paeth. I didn’t pursue that approach, but someone else may find it worthwhile.
Ok, that’s enough. Thanks for reading,
Jeremy